目次
Kaggleとは
機械学習を少し学んだらデータを使って試してみたいと思うと思いますが、適切なデータを探し出すのはなかなか困難な作業となります。そもそも、機械学習とは8割がデータ集めと言われているくらいなので、ホイホイ見つかるわけではないですよね。そんな時はkaggleにチャレンジしてみましょう。英語なのが少し難点ですが、簡単に書いてあるので頑張ってみましょうね。
その前に、Kaggleとは?っていう説明から入りましょう。
Kaggleとは、「13万人以上の参加者数を誇る世界最大の機械学習・データ分析コンペティションのためのプラットフォームです」、と書いてあるHPが多いですがその通りです(笑)。実力は関係なく初心者でも気軽にトライできますし、下で紹介しているタイタニックは誰もが分析したくなるデータをゲーム感覚でトライすることができます。2017年にあのGoogleが数百億円で買収したということで話題にもなりました。
あまりにも夢中になって仕事中も仕事するふりをしながらとらいしてしまったりするかもしれません。そんなことはないようにしましょうね。
ログインしてみよう
上記からログインしましょう。メールアドレスやFacebook、GoogleのIDからログインすることができるので、アカウントを申請しましょう。
さあ腕試し! タイタニックの生存する乗客を予測しろ!
まず最初の導入は、機械学習を使ってタイタニックの乗客2224人のデータから生存者を予測するモデルを作るというものです。導入なので少し英語を解説しますね。
まずこのタイタニック生存者予測は伝説的な機械学習コンペとなっています。皆さんもご存じのタイタニック映画なので目的がすごくわかりやすいことでも取り組みやすいテーマとなっているかと思います。
ビデオを見るとより理解が深まるとのことですが、機械学習はそもそもとても楽しいことや、どうやってスコアをあげるかの導入から始まり、次にどのようなカテゴリーの人物が生存するか(しやすいか)ということを予測するモデルを作ることというタイタニックコンペのルール説明があります。
コンペの進め方
1.ルールを理解してコンペに参加しよう
2.データをダウンロードしよう
3.問題を理解しよう
4.データ分析の冒険開始
5.機械学習モデルでアンサンブルを奏でよう
6.モデルをkaggleにアップロードして点数をみてみよう
ってyoutubeで説明されます。
そしてアレクシーというお姉さんにガイドしてもらうことを薦められます(笑)。
※怪しくないですよ
ここまでくればやってみようと思いました?
さあ一緒にチャレンジしてみましょう!
模範となるコードで勉強しよう
Kaggleのいいところは、模範となるモデルが数多く掲載されているところです。
Jupyter Notebookを使っている方にはなじみの深いコードで紹介されているため、自分のPCに落とし込んで勉強することができるようなサイトになっています。
もちろん自分でトライしてからにしてくださいね~。
ルールをきちんと把握しておこう
英語を読むのが苦手な方のためにルールを少し日本語で紹介しますね。
読むのが面倒だと思うので手短に。
マルチアカウントは禁止となっています。
複数アカウントで上限以上の件数をアップロードすることは禁止です。
コードはみんなで共有できる場合のみ紹介してよいです。逆にいうと、チーム外へのプライベートなコードやデータのやりとりは、KaggleのForum以外では禁止されており、また将来的にチームを組むことにしていてもチームを作る前に情報交換を行ってはいけません。
チームの合併はチームリーダが実施できます。
合併するためには、結合されたチームの総投稿数が合併期限の時点で認められている最大投稿数以下でなければなりません。認められている上限は、1日あたりの提出数に大会開催日数を乗じたものです。
チームの最大人数は5人までとなっています。
1日最大10件、最終的には5件の提出が可能です。
提出期限(このタイタニックの場合は時間制限なし)
最初はチームを作る(仲間を作る)という行動はしないと思いますので、
慣れてきたらやっていけばよいかと思いますよ。
データをダウンロードして冒険を開始しよう
ルールを理解したら、「ルールを理解しましたボタン」をおしてデータのダウンロードを始めましょう。3種類のデータがあると思います。
①「train.csv」
1~891番までの乗客の情報 + 生死の情報
②「test.csv」
892~1302番までの乗客の情報
③「gender_submission.csv」
892~1302番までの乗客の生死の情報の解答例 (※あくまで例です:答えではないですよ)
①のデータを解析して予測モデルを作成し、②の情報の人々の生存予測を立て、③のような解答事例を作成するというルールになっています。
それにしても、早速基本的なデータの処理能力を試してきましたね~。このサイトでも紹介しているPandas,Numpyでのデータ処理を駆使して機械学習できる状態までもっていきましょう。
情報前処理と可視化
まずは情報の前処理と可視化ですね。JypyterNotebookを立ち上げて進めていきますが、簡単なデータなので一度覗いてみることが重要です。上で説明してしまいましたが(笑)、データは3つ。それぞれの情報がバラバラになっていることから前処理が必要となってきます。
そのまえに、、
ですが、Pythonを勉強されている方はライブラリのimportをする必要があることは理解されていると思いますが、機械学習も数多くのライブラリが用意されており、わからないうちはデフォルト的にimportしておくことをおすすめします。
# セル1
# モジュールの読み込み
import numpy as np
import pandas as pd
import matplotlib.pyplot as pltNumpy,Pandas,matplotlibはこのサイトでも説明していますので、そちらを参考にしてくださいね。
情報前処理①
次にデータを読み込んでいきます。
# セル2
# データの読み込み
df_train = pd.read_csv('train.csv')
df_test = pd.read_csv('test.csv')ここからがデータ処理の頭の使いどころです。今回データから読み取れる情報としては
■乗客通し番号
■等級(1等級、2等級、3等級)
■名前
■性別
■年齢
■SibSp 兄弟、配偶者の数
■Parch 両親、子供の数
■チケット番号
■料金
■部屋番号
■乗船した港
C = Cherbourg, Q = Queenstown, S = Southampton
となっています。
ここでデータの前処理をもう少し進めていきますね。
# セル3
# type が空(na)だったら unknown にする(fillna()メソッド)
df_train['Sex'] = df_train['Sex'].fillna('unknown')
df_train['Embarked'] = df_train['Embarked'].fillna('unknown')
df_train['Pclass'] = df_train['Pclass'].fillna('unknown')
# セル4
# typeが空(na)だったら平均値を入れる 年齢と運賃
df_test['Age'].fillna(df_test['Age'].mean(), inplace=True)
df_test['Fare'].fillna(df_test['Fare'].mean(), inplace=True)
# セル補足(下記は年齢を10歳おきに仕分け)
df_train['Age_class'] = round(df_train['Age']/10)*10
df_test['Age_class'] = round(df_test['Age']/10)*10
# セル5
# 必要columnsのみを選択
df_train = df_train[['Survived', 'Pclass', 'Sex', 'Age', 'SibSp',
'Parch', 'Fare', 'Embarked','Age_class']]
df_test = df_test[[ 'Pclass', 'Sex', 'Age', 'SibSp',
'Parch', 'Fare', 'Embarked','Age_class','PassengerId']]
# セル6
# 欠損値がある行を削除
df_train = df_train.dropna()データの可視化と目途付け
ここからがデータ分析の力量が試されるところですが、まずはどんな因果関係があるか、そもそもどんな乗客構成だったか等を知りたいですよね。そこでmatplotlib,seabornを使ってみていきましょう。グラフモジュールを下記コードで読み込んでください。
# グラフモジュールの読み込み
import matplotlib.pyplot as plt
import seaborn as sns次にグラフを作成していきます。
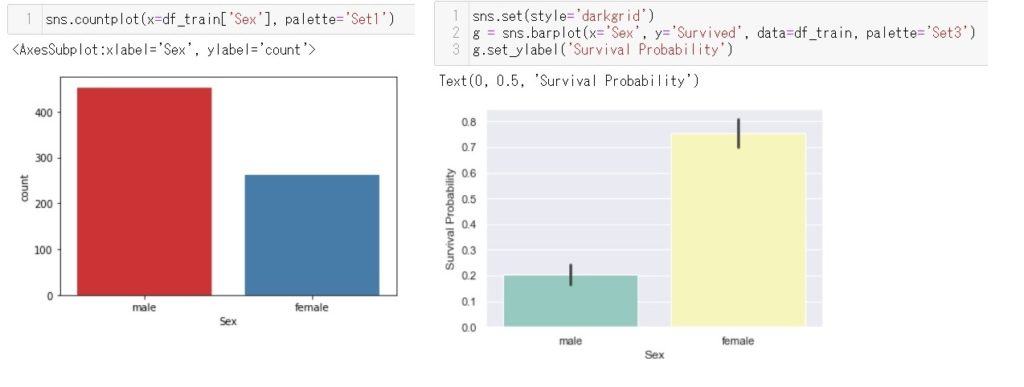
下記左図は男性と女性の人数、下記右図は男性と女性のそれぞれの生存率です。圧倒的に女性の生存率が高いんですね。映画ではLadyFirstで救命ボートに乗せていましたがそれを物語るデータとなっていることがわかりますね。コードはそれぞれのグラフの上に記載してあります。
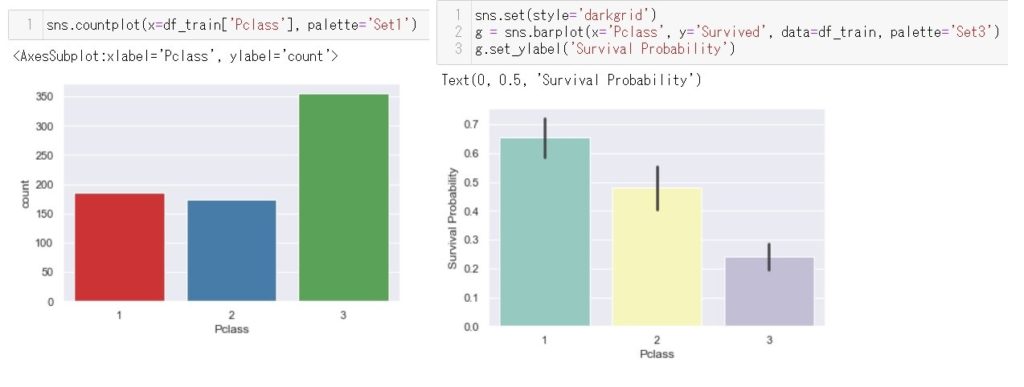
同様にグラフを作りましょう。今度は客席等級の分布です。ここでも1等級から3等級にかけて生存率が減少していくのが見て取れます。分析のヒントになりますよね~。
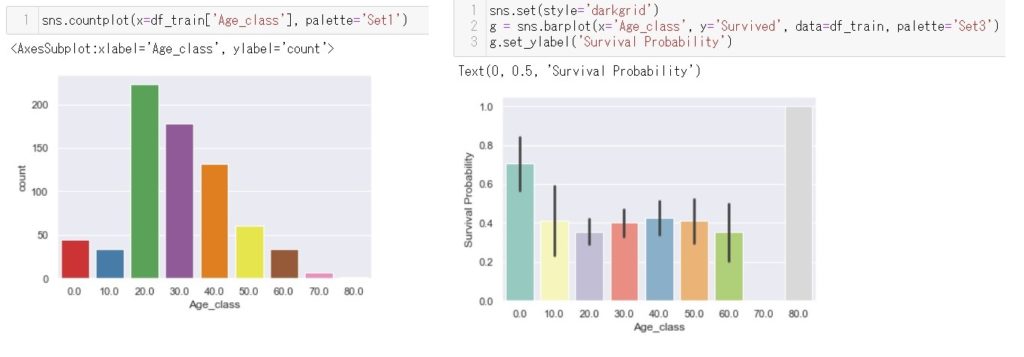
最後に年齢です。10歳以下の生存率が高い以外はあまり年齢では変わらないですね。ここは少し以外でもう少し高齢の方の生存率が高いかと考えていました。
sns.countplot(x=df_train['Sex'], palette='Set1')
sns.set(style='darkgrid')
g = sns.barplot(x='Sex', y='Survived', data=df_train, palette='Set3')
g.set_ylabel('Survival Probability')
sns.countplot(x=df_train['Pclass'], palette='Set1')
sns.set(style='darkgrid')
g = sns.barplot(x='Pclass', y='Survived', data=df_train, palette='Set3')
g.set_ylabel('Survival Probability')
sns.countplot(x=df_train['Embarked'], palette='Set1')
sns.set(style='darkgrid')
g = sns.barplot(x='Embarked', y='Survived', data=df_train, palette='Set3')
g.set_ylabel('Survival Probability')
sns.distplot(df_train['Age'], kde=False, bins=8, color='blue')
sns.countplot(x=df_train['Age_class'], palette='Set1')
sns.set(style='darkgrid')
g = sns.barplot(x='Age_class', y='Survived', data=df_train, palette='Set3')
g.set_ylabel('Survival Probability')
sns.factorplot(x='Pclass',y='Age', hue='Sex', data=df_train,palette='pastel')情報前処理②
目途がついてきたところでもう少し前処理を実施していきます。
# セル7
# ワンホットエンコーディング
# dummy_na=Trueで欠損値はダミー変数の列を作ります
X_dummies = pd.get_dummies(df_train, dummy_na=True, columns=['Sex', 'Embarked', 'Pclass'])
XX_dummies = pd.get_dummies(df_test, dummy_na=True, columns=['Sex', 'Embarked', 'Pclass'])
#セル8 Embarkedがunknownの行を削除する
X_dummies= X_dummies[X_dummies['Embarked_unknown'] != 1]
#セル9 df1、df2をそれぞれ必要なcolumnsのみにする
df1 = X_dummies[
['Survived', 'Age', 'SibSp', 'Parch', 'Fare', 'Sex_female', 'Sex_male',
'Embarked_C', 'Embarked_Q', 'Embarked_S',
'Pclass_1.0', 'Pclass_2.0', 'Pclass_3.0']
]
df2= XX_dummies[
['Age', 'SibSp', 'Parch', 'Fare', 'Sex_female', 'Sex_male',
'Embarked_C', 'Embarked_Q', 'Embarked_S',
'Pclass_1.0', 'Pclass_2.0', 'Pclass_3.0','PassengerId']
]これでいよいよ前処理完了です。
決定木によるモデル作成
モデル作成準備
ここからいよいよモデルの作成です。今回は生死を判断するモデルをつくるので決定木のモデルを作成していくことにしましょう。ここからは初心者のかたは写経をするイメージでうつしてください(笑)。コピペもいいですが少しづつ勉強することが大事と思いますので。
機械学習初体験のかたはここからいよいよコーディングを通じて勉強していきましょう。ある程度理解している方は「ふむふむ」という感じで見ていってくださいね。まずは説明変数と目的変数に分けます。目的変数はもちろん[‘Survived’]ですよね。分割するモジュールも読み込んで分けてしまいます。ここではtest_size=0.2としており、8:2の割合で分けることにしました。
#セル10 説明変数と目的変数
X = df1[['Age', 'SibSp', 'Parch', 'Fare', 'Sex_female', 'Sex_male',
'Embarked_C', 'Embarked_Q', 'Embarked_S',
'Pclass_1.0', 'Pclass_2.0', 'Pclass_3.0']]
Y = df1['Survived']
# セル11
# 学習データとテストデータに分割するためのモジュール読み込み
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)次にモジュール読み込みです。
ここは写経の時間かと思います。あまり何も考えずうつしましょう。
# セル12
# 決定木モジュール
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
# グリッドサーチモジュール
from sklearn.model_selection import GridSearchCV
# 決定木モデル描画のためのモジュール
import pydotplus
import io
from IPython.display import Image
# 混同行列モジュール
from sklearn.metrics import confusion_matrix
# その他モジュール
from sklearn.metrics import accuracy_score
from sklearn.metrics import recall_score
from sklearn.metrics import precision_score
from sklearn.metrics import f1_score決定木によるモデル作成
いよいよモデル作成です。グリッドサーチで最適パラメータをみつけ、それによるモデル作成という手順で進めていきます。グリッドサーチを簡単に解説しておくと、すべてのパラメータを総当たりで組み合わせを試すことにより一番適したパラメータを見つけ出すという荒業です……。こんなことは手作業では決してできません。この辺がSQCとは違うところと言えるかもしれません。デメリットは時間がかかることですが、今回はそんな大きなモデルでもないのでこれを選択します。
# セル13
# 閾値を設定(木の深さ:最大10,葉(末端)のデータ数:最小30)
# モデル作成準備(閾値の範囲を指定)
param_grid = {'min_impurity_decrease':np.arange(0.0,0.04,0.001)} # 0.00~0.04の間で0.001ずつ網羅
# モデル作成準備(グリッドサーチで探査)
mdl_1 = GridSearchCV(
DecisionTreeClassifier
(max_depth = 10, min_samples_leaf = 30),
param_grid, cv = 5, scoring = 'accuracy'
)
# モデル作成準備
mdl_1.fit(X_train, Y_train)
# モデルの情報の表示
print(mdl_1.__class__.__name__)
print("最適なパラメーター =", mdl_1.best_params_,
"Accuracy(正解率) =", f'{mdl_1.best_score_:.03f}')
# グリッドサーチの結果
pd.DataFrame(mdl_1.cv_results_).head()
# 1番よかった決定木を指定
mdl_1.best_estimator_実行してみれば最適パラメータを見つけてくれます。
おそらく、
‘min_impurity_decrease’が0.003、
正解率が0.79
ぐらいででてくるのではないでしょうか?
ここで正解率の目途もつけることができます。
次に決定木を表示させます
# セル14
# 作成した決定木モデル
dot_data = io.StringIO()
tree.export_graphviz(mdl_1.best_estimator_, out_file = dot_data, feature_names = X_train.columns,class_names = ['Dead', 'Alive'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.progs = {'dot': u"C:\\Program Files\\graphviz\\bin\\dot.exe"}
Image(graph.create_png())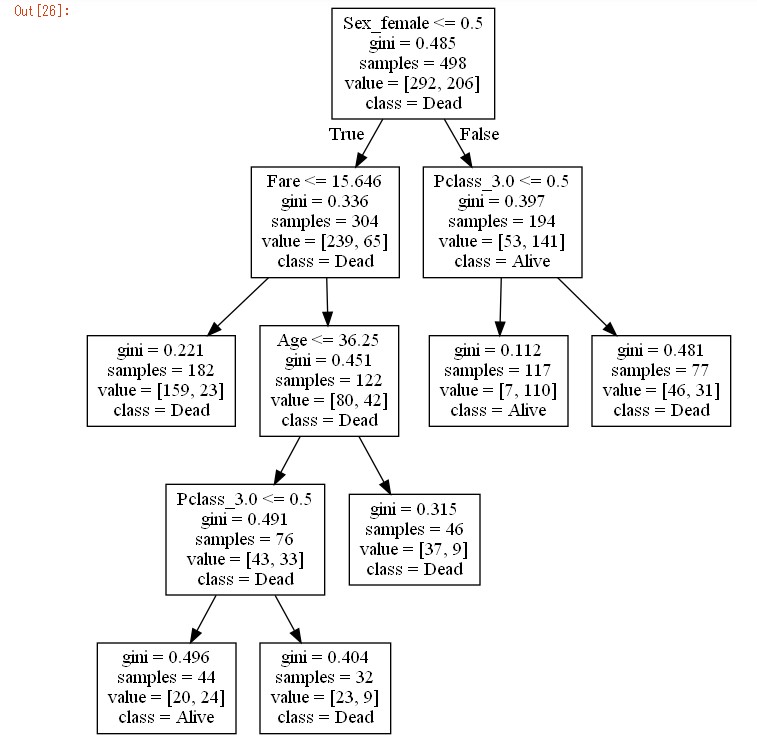
ここまでくるとやった甲斐がありますよね~。性別で最初にわかれたあと、料金、客室等級、年齢で分岐されています。
# セル15
# 説明変数の重要度
print("説明変数の重要度")
feature_importance = pd.DataFrame(mdl_1.best_estimator_.feature_importances_)
feature_importance.index = X_train.columns
feature_importance.columns = ['feature importance']
print(feature_importance)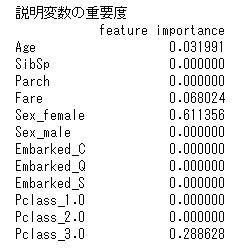
説明変数の重要度は、決定木でもつかわれていた、性別、料金、客室等級、年齢以外は0となっており関係ないことがわかります。
# セル16
# 分類結果:学習データ
# 学習データの分類予測
predict_train_1 = mdl_1.best_estimator_.predict(X_train)
# 学習データの混同行列
cm_train_1 = confusion_matrix(Y_train, predict_train_1)
print('混同行列 0:Negative, 1:Positive')
print('[ [TN,FP]')
print(' [FN,TP] ]')
print('\n混同行列:学習データ')
print(cm_train_1)
# 分類結果の評価:Accuracy(正解率),Recall(再現率),Precision(適合率),F_measure(F値)
print('\nAccuracy(正解率):学習データ = ',f'{accuracy_score(Y_train, predict_train_1):.03f}')
print('Recall(再現率):学習データ = ',f'{recall_score(Y_train, predict_train_1, pos_label=1):.03f}')
print('Precision(適合率):学習データ = ',f'{precision_score(Y_train, predict_train_1, pos_label=1):.03f}')
print('F_measure(F値):学習データ = ',f'{f1_score(Y_train, predict_train_1, pos_label=1):.03f}')
つづいて混同行列です(混同行列詳細はこちら)。
正答率は80%を超えなかなかのモデルができたのではないかと思います。
# セル17
# 分類結果:テストデータ
# テストデータの分類予測
predict_test_1 = mdl_1.best_estimator_.predict(X_test)
# テストデータの混同行列
cm_test_1 = confusion_matrix(Y_test, predict_test_1)
print('混同行列 0:Negative, 1:Positive')
print('[ [TN,FP]')
print(' [FN,TP] ]')
print('\n混同行列:テストデータ')
print(cm_test_1)
# 分類結果の評価:Accuracy(正解率),Recall(再現率),Precision(適合率),F_measure(F値)
print('\nAccuracy(正解率):テストデータ = ',f'{accuracy_score(Y_test, predict_test_1):.03f}')
print('Recall(再現率):テストデータ = ',f'{recall_score(Y_test, predict_test_1, pos_label=1):.03f}')
print('Precision(適合率):テストデータ = ',f'{precision_score(Y_test, predict_test_1, pos_label=1):.03f}')
print('F_measure(F値):テストデータ = ',f'{f1_score(Y_test, predict_test_1, pos_label=1):.03f}')テストデータの結果は飛ばしますね。
ここは自分で確認してみてください。
予測の実施とkaggle提出データ作成
つづいてはtestデータをモデルに合わせて予測をしていきます。
# セル18
df22=df2[
['Age', 'SibSp', 'Parch', 'Fare', 'Sex_female', 'Sex_male',
'Embarked_C', 'Embarked_Q', 'Embarked_S',
'Pclass_1.0', 'Pclass_2.0', 'Pclass_3.0']
]
# 予測を実施
predict = mdl_1.predict(df22)最後に予測したデータをcsvに書き出して完成です。
# セル19
# 予測値を乗客IDに合わせてcsvを作成し書き出し
submit_csv = pd.concat([df2['PassengerId'], pd.Series(predict)], axis=1)
submit_csv.columns = ['PassengerId', 'Survived']
submit_csv.to_csv('submition.csv', index=False)ちなみにこの結果14741位です……。まあなにも工夫していないので当然かもしれませんが。これすごいのはTOPは100%の正解率なんですがどうやって導き出しているか勉強してみたいですよね。どうやら名前にも色々ヒントが隠されているらしく、やればやるほど正解率を上げることができるkaggle少しはまっていきそうです。
いずれにしても、ここまで読んでもらった皆さんありがとうございます!
そして、お疲れさまでした!



コメント
[…] […]