Kaggleコンペ挑戦シリーズ第2弾です。今回は前回のタイタニック(分類タスク)と違い回帰タスクです。様々な条件から家の販売価格を推測するというものです。早速始めていきましょう。
「キヨシの命題」さんがとても参考になりました。
参考にしながら解きましたよ (^^♪
そもそもKaggleとはなにか、ログイン方法は下記を参考にしてくださいね。
さて、Kaggleにチャレンジし始めタイタニックを解き終わった後、どのようなコンペにチャレンジすればよいかを悩んでいる人は多いのではないでしょうか?ここは迷うことなくこの「住宅価格予測コンペ」にチャレンジしてください。タイタニックは分類回帰(「0」か「1」のどちらかを推測)の導入コンペですが、住宅予測コンペは回帰タスク(数値を予測)の導入コンペの位置づけとなっており、Kaggle攻略本もこのコンペを採用していることが多いです。そういう意味でこのコンペはおすすめですよ!
目次
様々な条件から住宅価格を予測せよ!
今回のコンペは様々な条件にたいする住宅価格データを活用して、わかっていない住宅価格を予想するというチャレンジです。タイトルは「House Prices – Advanced Regression Techniques」です。
kaggleはすべて英語なので(笑)、導入で書いてあることを少し解説していきますね。
住宅を購入し人生に夢を持った購入者のために価格を予測していくという設定です。地下室の天井の高さや、東西に走っている鉄道との距離といった、住宅価格を決定する上で重要であろう説明変数を活用しながら進めていくことをおすすめしています。ただ、このデータは寝室の数、白い柵よりもはるかに多くの説明変数が住宅価格に影響を与えることが証明されている、とのこと。アイオワ州エイムズの住宅を79の説明変数を使用して各住宅の予想価格を求めてください。
とのことです。早速始めていきましょうか。
データをダウンロードして確認してみよう
データダウンロードのサイトに行くと4種類のデータがあると思います。
①「train.csv」
1~1460番までの説明変数 + 住宅価格 の情報
②「test.csv」
1461~2919番までの説明変数
③「sumple_submission.csv」
1461~2919番までの住宅価格解答例 (※あくまで例です:答えではないですよ)
④「data_description.txt」
79の説明変数の解説
Titanicと同じく、①のデータを解析して予測モデルを作成し、②の情報の人々の生存予測を立て、③のような解答事例を作成するというルールになっています。
情報前処理と可視化
機械学習での情報前処理は、モデルを決定する上で非常に重要です。一般的に情報前処理が8割の工数を占めると言われています。しっかりデータを理解し進めることが必要となります。
ここでは、79も説明変数があるのですが、ご丁寧に今回説明変数の解説が添付されていますよね(笑)。こんな重要情報が普通はついていませんし、業務で活用するときは情報収集がそもそも大変なのに……。まあそれはおいておいて、せっかく添付されているので解説していきましょう。
79の説明変数を解説するだけでひとつの記事になってしまいました(笑)。内容が濃すぎますよね。ここでの記事は回帰タスクを活用しての数値予測を一通り理解してもらいたいと思いますので、まずは欠損値をあまり考えずに埋めていくということで進めていきます。
まずは必要モジュールのインポート、データの読み込み、から進めましょう。
# 共通モジュールのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib #matplotlibの日本語対応
import seaborn as sns
# matplotlibを作動させる呪文
%matplotlib inline# データの読み込み
df_train = pd.read_csv('train.csv')
df_test = pd.read_csv('test.csv')ここでは、あまりデータの可視化について説明しませんが、ヒストグラムの表示のさせ方と、すべてのデータの相関係数の出し方を紹介しておきます。良いモデルを作成していくためにはここで様々な手法を活用しデータの見える化と前処理をしていかないといけないですが、またにさせてください。
# ヒストグラムを表示させて見える化
sns.distplot(df_train['SalePrice'])
# 対数変換して正規分布に近づける
sns.distplot(np.log(df_train['SalePrice']))
# すべてのデータ同士の相関係数
df_train.corr()
# CSVに書き出す
df_train.corr().to_csv('df_train.corr1.csv', index=True)
# 学習データ、テストデータの行列(データ数、因子数を把握)を表示
print('trainデータ(データ数,因子数) : ' + str(df_train.shape))
print('testデータ(データ数,因子数) : ' + str(df_test.shape))見える化やや不十分ですが、情報の前処理に進んでいきましょう。
情報前処理(One-hotエンコーディング)
この作業は大事なのでぜひ自分のものにしてください。
One-hotエンコーディングとは、カテゴライズ化ともいわれていますが、objectのデータをカテゴリを列に展開し、それぞれに0/1を割り当てるという作業です。これにより、object型の文字列を機械的に処理できるようにします。
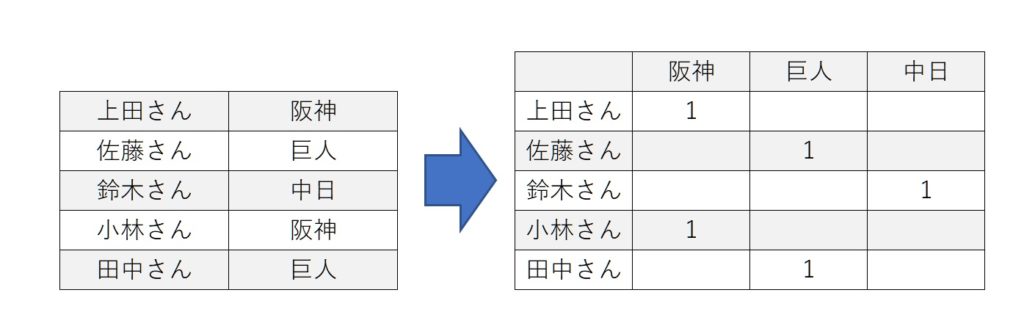
上記がイメージとなります。
ここで一つポイントは今回train、testとデータが2つに分かれていますが、まずマージすることをおすすめします。One-hotエンコーディングでカテゴライズ化をしますが、2つのデータで共通のカテゴライズ化ができるとは限らないからです。上記の例でいうと、片方のデータには「阪神」「巨人」、もう一つのデータには「阪神」「中日」となると、モデルと作った際に予測ができないということになってしまうからです。
それでは始めていきましょう。
# 学習データとテストデータのマージ
# → 前処理を同時にするため one-hotエンコーディングをする場合ずれが生じないためこちらがよい
df_train['Data_from'] = 'Train'
df_test['Data_from'] = 'Test'
df_test['SalePrice'] = 1000000000
df_all = pd.concat([df_train,df_test],axis=0).reset_index(drop=True)次に欠損値の処理をします。ここではデータ型に応じて、float64は「0」を、object型は「NA」を代入します。
# 欠損を含むカラムのデータ型を確認
list_columns_na = df_all.isnull().sum()[df_all.isnull().sum()>0].index.tolist() # 欠損を含むカラムをリスト化
# データ型に応じて欠損値を補完する、まずデータ型に対応したカラムリストを作成する
list_columns_float = df_all[list_columns_na].dtypes[df_all[list_columns_na].dtypes=='float64'].index.tolist() #float64
list_columns_obje = df_all[list_columns_na].dtypes[df_all[list_columns_na].dtypes=='object'].index.tolist() #object
# float64型で欠損している場合は0を代入
for Na_float in list_columns_float:
df_all.loc[df_all[Na_float].isnull(),Na_float] = 0.0
# object型で欠損している場合は'NA'を代入
for Na_obj in list_columns_obje:
df_all.loc[df_all[Na_obj].isnull(),Na_obj] = 'NA'いよいよ「One-hotエンコーディング」です
# One-hotエンコーディングをする変数のカラム名(特徴量)をリスト化
onehot_cols = df_all.dtypes[df_all.dtypes=='object'].index.tolist()
# 数値変数のカラム名(特徴量)をリスト化
num_cols = df_all.dtypes[df_all.dtypes!='object'].index.tolist()
# データ分割および提出時に必要なカラムをリスト化
other_cols = ['Id','Data_from']
# 不要な要素をリストから削除
# それぞれのデータ型に応じて不要なデータが入っているため削除する
onehot_cols.remove('Data_from') #学習データ・テストデータ区別フラグ除去
num_cols.remove('Id') #Id削除
# カテゴリカル変数をダミー化
df_all_onehot = pd.get_dummies(df_all[onehot_cols])
# データ統合
all_data = pd.cononehot([df_all[other_cols],df_all[num_cols],df_all_onehot],axis=1)# マージデータを学習データとテストデータに分割
train_ = all_data[all_data['Data_from']=='Train'].drop(['Data_from','Id'], axis=1).reset_index(drop=True)
test_ = all_data[all_data['Data_from']=='Test'].drop(['Data_from','SalePrice'], axis=1).reset_index(drop=True)
# 学習データ内の分割
train_x = train_.drop('SalePrice',axis=1)
train_y = train_['SalePrice']
# テストデータ内の分割
test_id = test_['Id']
test_x = test_.drop('Id',axis=1)scikit-learnを活用してモデルを作成しよう!
scikit-learnとは「Pythonの代表的な機械学習のライブラリ」です。また詳しくはご紹介していこうと思いますが、scikit-learnを使うと、簡単に機械学習を試してみることができます。
モデルの作成、定義
まずライブラリを読み込んでいきましょう。
# 標準化ライブラリ
from sklearn.preprocessing import StandardScaler
# 訓練データ、テストデータに分類するモジュール
from sklearn.model_selection import train_test_split
# RMSEを算出するモジュール
from sklearn.metrics import mean_squared_error
# モデル作成するモジュール
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import (
LinearRegression,
Ridge,
Lasso
)あまりにも多くの手法があるので、ここでは代表的な3つを紹介したいと思います。
【A】線形回帰モデル(基本形)
【B】リッジ回帰
【C】ラッソ回帰
モデルを作っていくことになるのでコードを記載します。詳細は別記事で解説していきますので、好きな(といってもどれがどうかわからないかもしれませんが)を選んでコードを記載してください。
ここで合わせて、下記のDataFrameも作っていきます。
X_std trainの特徴量
XX_std testの特徴量
Y_std trainの正解データ
#【A】線形回帰モデル(基本形)
# モデル設定
mdl = LinearRegression()
# データ整理①
X_dummies = train_x
Y = train_['SalePrice']
XX_dummies = test_x
# データ整理②
X_std = X_dummies
XX_std = XX_dummies
Y_std = Y#【B】リッジ回帰
# モデル設定
mdl = Ridge(alpha = 10)
# データ整理①
X_dummies = train_x
Y = train_['SalePrice']
XX_dummies = test_x
# データ整理②
X_std = X_dummies
XX_std = XX_dummies
Y_std = Y#【C】ラッソ回帰
# モデル設定
mdl = Lasso(alpha = 0.1)
# データ整理①
X_dummies = train_x
Y = train_['SalePrice']
XX_dummies = test_x
# データ整理②
X_std = X_dummies
XX_std = XX_dummies
Y_std = Yモデルの実行
学習データとテストデータに分けていきます。
機械学習(教師あり)では、データをある一定の割合で学習データとテストデータに分類します。ここでは3割をテストデータに分類しています(test_size=0.3)。
# train_test_splitを用いて学習データとテストデータを分ける
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test=train_test_split(X_std, Y_std, test_size=0.3, random_state=77)
#randam_stateを指定しすることで、乱数を固定することができるいよいよモデルの実行です。
mdl.fit(X_train, Y_train) #学習の実行たった1行?と思うかもしれませんが、これで終了です。モデルを作成することができました。ただ、このモデルを評価する必要があります。先ほどtrainデータとtestデータに分けたかと思いますが、そのtestデータを使って検証していくことになります。「寄与率」を用いて評価します。0.6を超えるとそれなりに良いモデルができているといわれています。
decimal_p = 3 #小数点以下の桁数
print('寄与率:', mdl.score(X_train,Y_train)) #0.6を超えるとよいモデルtestデータの予測と汎化性能の検証
モデルが完成したので早速予測していきましょう。
#推論の実行
Y_pred = mdl.predict(X_test)ここも予測は1行で終了です。
ただし、重要なことがあります。汎化性能です。与えられた訓練データを再現する力の事を表現力と呼びます。 使うモデルの表現力が高すぎると、データの些細な挙動までモデルが学習してしまい、未知のデータの予測が難しくなります。 データに含まれる誤差の部分を無視する力を汎化性能と呼びます。がgoogle先生からの抜粋です(笑)。
要するに作成してモデルが過学習していないか、いろいろなデータを予測した際にまんべんなく予測できるか、という日本語が一番わかりやすいかと思います。よくr2スコアが用いられます
from sklearn.metrics import r2_score
r2_score = r2_score(Y_test, Y_pred) #真値と予測値のスコア算出
print('r2スコア:', r2_score)最後にコンペに提出するデータを作成してみましょう。
YY_pred = mdl.predict(XX_std) #推論の実行(testデータの予測コード→コンペに提出する予測値の作成)
# 予測値をIDに合わせてcsvを作成し書き出し
submit_csv = pd.concat([df_test['Id'], pd.Series(YY_pred.flatten())], axis=1)
submit_csv.columns = ['Id', 'SalePrice']
submit_csv.to_csv('submition-House.csv', index=False)これで完了です。





コメント